概要の紹介です．利用方法は こ ちらへ．

第１章

２次元

地球上の点を２つの数字で表す方法をヒッパルコスが説明する…

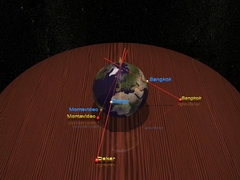…そして，ステレオグラフ射影を教える：世界地図作成の方法である．

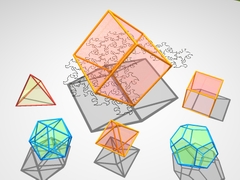
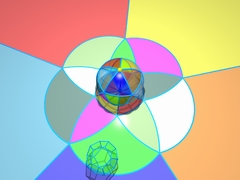
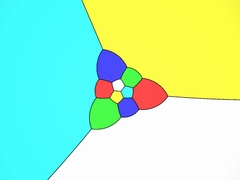
第２章

３次元

３次元の図形を理解しようとする２次元の生き物の冒険をエッシャーが語る．

第３章，第４章

第４次元

数学者ルートヴィヒ・シュレフリが，第４の次元の図形を語る…

…そして４次元の正多面体を紹介する：２４個，１２０個，６００個もの面をもつ不思議 な図形である！

第５章，第６章

複素数

数学者アドリアン・ドゥアディーが複素数を説明する．負の数の平方根が平易に説明される．

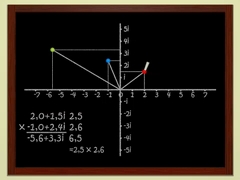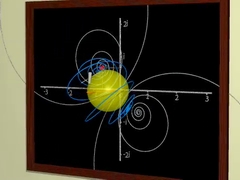平面を変換する，画像を変形する，フラクタル図形を生成する…

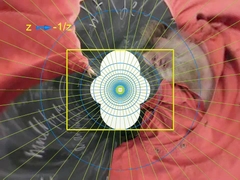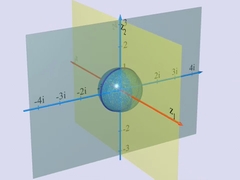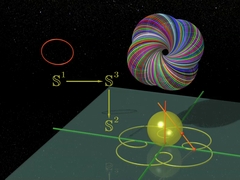
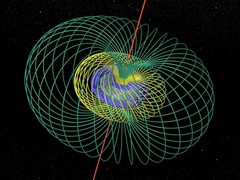
第７章，第８章

ファイブレーション

数学者ハインツ・ホップが「ファイブレーション」を解説する． 複素数を使って，彼は空間内に美しい円周の配置をつくりあげる．

円周，トーラス…，すべてが４次元空間で回転する！

第９章

証明

数学者ベルンハルト・リーマンが，数学における証明の重要性を語る．ステレオグラフ射影についてのひとつの定 理が証明される．

このビデオの利用方法

このビデオは，（理解しようという方には，）その人にあった章を選んで見てもらえれば，どなたにでもお楽しみ いただけるように作られています． ビデオは９つの章からなっており，各章の長さは１３分です． ３－４章，５－６章，７－８章は，つながっていますが，それ以外は，ほぼ独立しています．

もちろん，テレビ画面やパソコンのモニターに向かって，１１７分のビデオを一気に見るのもよいでしょう！ でも，あなたにとっては，場面展開が速すぎるところもあるかもしれませんし，他のところは簡単過ぎるかもしれません． それは，あなたの関心や予備知識によりますし，単にそのときの気分にもよるでしょう！… あなたに合った章をよく選んで見ることもできます． ここでは，ビデオをよく理解できるような見方を説明します． もう少し説明が必要なら，説 明のページをご覧ください． そのページにもビデオの場面が出ています…

おおまかに言うと，章を追うごとに数学のレベルが少しずつ上がってい きます：

第１章，「２次元」は，難し くありません． この章は，中学生でも十分わかるはずです． しかし，経線と緯線を知っている方でも，地球がボールのように転がる様子は，面白いと思うことでしょう！ （ここを ご覧ください）．

第２章， 「３次元」も，難 しくありませんが，少し想像力を働かせる必要があります． スペクタクルと思ってみても良いですが，少し哲学的なものを含んでいます… 練習問題もあって，理解できたかどうか確かめることもできます． 説明，補足，参考文献については，このサイト内のこ のページをご覧ください．

第３章，第４章では，「第４次元」 を紹介します． もちろん，もっと難しいことですし，頭がくらくらするかもしれません． すべてを理解するために，ビデオのコントローラのボタンを押して何度も繰り返して見たり，このページにある補足説明や，それの参考文献を参照してください． しかし，全部を理解する気がなくなっても，映像の美しさは堪能できます！

第５章，第６章，「複素数」 では，フランスでは高等学校で教わる複素数を説明します． この説明は，授業で教わることの代わりになるというものではなく，授業の良い補足となるだろうと思います． ずっと前に複素数を勉強して，もう忘れてしまった…という人には，思い出す助けになるでしょう． もしも，複素数をまったく知らなければ，コントローラの停止ボタンを何度も押して，私達がお勧めする参考文献を参照しな がら理解する努力をしてください． この２つの章は，このビデオの中でもっとも「学校の授業」に似ています． そんな努力をしてもらう代わりに，第６章の最後には，驚くべき深さまでズームアップする映像をご覧いただけます．

第７章，第８章は「ホップ・ファイブレーション」 の紹介です． これは，高校では習わないし，大学の１，２年生でも習わないものです． つまり，本当に初めての人を対象にしているのではないということになります． しかし，映像は美しく，理解する努力をする価値が十分にあるものです． ところどころに説明が速すぎるところはありますが，必要なことはすべて説明されています． ここでも，何か難しいところがあれば参 考文献が役に立つでしょう…　 理解しようと頑張りながら，美しい映像を見てください！

最後に，第９章は，特別な章です．そこでは「幾何 的な定理の証明」をおこないます． この証明は，中学生で習うことしか使っていませんから，第１章の次にきても良い内容です． 定理を証明することがなければ，数学は存在しません． このビデオは数学的対象を映像化しているのですから，このビデオの最後で，そのことをはっきりさせておきたいと思います（ここをご覧くださ い）．

章の選び方の例：

中学生： 1, 1-2, 1-2-9
高校生： 1-2-(3-4)-9
理科系の高校生： 5-6
理科系の大学１，２年生： 2-3-4-5-6 あるいは 5-6-(7-8-9)
理科系の大学３，４年生： 7-8-(9)
一般： 1-2-3-4-(9)