Veja o conteúdo do filme, ou vá para o guia de utilização do filme

Capítulo 1

A dimensão dois

Hiparco explica como localizar um lugar na Terra a partir de dois números.

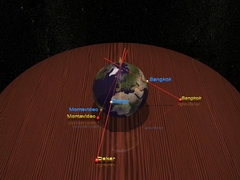...e mostra através da  projeção estereográfica como desenhar um mapa-mundi.

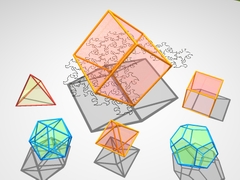
Capítulo 2

A dimensão três

M.C. Escher conta aventuras de criaturas de dimensão 2 que procuram imaginar objetos de dimensão 3.

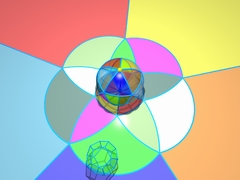
Capítulos 3 e 4

A quarta dimensão

O matemático Ludwig Schläfli nos fala de objetos na quarta dimensão...

... e nos mostra um desfile de poliedros regulares, em dimensão 4, objetos estranhos com 24, 120 e mesmo 600 faces!

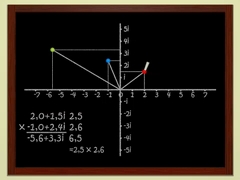
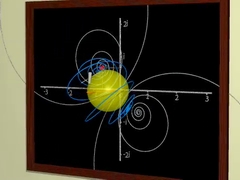
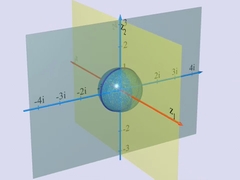
Capítulos 5 e 6

Números complexos

O matemático Adrien Douady explica os números complexos. A raiz quadrada de números negativos é explicada de forma simples.

Transformar o plano, deformar imagens, criar imagens fractais...

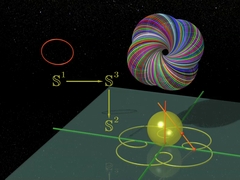
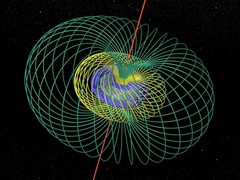
Capítulos 7 e 8

Fibração

O matemático Heinz Hopf descreve sua “fibração”. Graças aos números complexos ele constrói belos arranjos de círculos no espaço.

Círculos, toros, tudo girando no espaço... de dimensão 4 !

Capítulo 9

Uma prova matemática

O matemático Bernhard Riemann explica a importância das demonstrações em matemática. Ele demonstra um teorema sobre a projeção estereográfica.

Como utilizar este filme ?

O filme foi concebido para que todo público (quem quiser) possa apreciá-lo, escolhendo os capítulos que desejar! Compõe-se de 9 capítulos, cada um com duração de 13 minutos. De fato, os capítulos 3-4, 5-6 e 7-8 são capítulos duplos, mas os demais, são um pouco independentes.

Pode-se, em verdade, sentar-se diante de uma televisão ou computador e assistir durante 117 minutos ao conjunto de uma só vez!  Haverá, talvez, passagens que parecerão muito rápidas ou muito elementares. Isto vai depender do interesse de cada um, dos conhecimentos anteriores ou,   simplesmente, do humor do momento... É possível também se contentar com alguns capítulos bem escolhidos. Eis algumas indicações para ajudar no melhor aproveitamento do filme. Para saber um pouco mais, pode-se consultar as páginas de explicações onde se encontram também pequenos trechos do filme.
 

Ä grosso  modo, o nível matemático dos capítulos vai aumentando pouco a pouco:

O capítulo 1, a dimensão 2, é muito elementar. Poderia ser apreciado por alunos do ensino médio, mas pensamos que mesmo aqueles que já saibam o que sejam meridianos e paralelos gostarão, talvez, de ver o espetáculo da Terra que rola como uma bola ! (aqui).

O Capítulo 2, a dimensão 3,  é elementar mas exige um pouco de imaginação. Pode ser visto como um espetáculo, que incita um pouco à filosofia. Contém mesmo exercícios a fim de verificar se foi bem compreendido. Para explicações, complementos, referências adicionais, consultar esta pagina  neste sítio.

Os capítulos 3 e 4  nos apresentam a quarta dimensão. Certamente, é mais difícil e pode causar vertigens ? Se desejarem compreender melhor, não hesitem em utilizar a tecla pausa desta apresentação, rever muitas vezes este capítulo, consultar esta página na qual encontrarão referências para os complementos. Além disso, se não quiserem compreender tudo, poderão simplesmente admirar as imagens !

Os capítulos 5 e 6, números complexos,  apresentam uma introdução aos números complexos, que se aprende no ensino médio no Brasil. Não pretende substituir o curso clássico, mas pensamos que estes capítulos podem ser apreciados como complementos. Se estudaram os números complexos há muito tempo, e já se esqueceram... poderão refrescar a memória. Se não sabem nada sobre números complexos, é preciso utilizar a tecla de pausa muitas vezes e procurar compreender utilizando referências que  apresentamos .Estes capítulos são os mais escolares do filme. Para recompensar o esforço, no fim do capítulo, é apresentada  uma cena de  mergulho incrível.

Os capítulos 7 e 8 contêm uma introdução ä fibração de Hopf, que não é discutida no colégio, nem mesmo nos primeiros semestres do curso universitário. E, por isto, é claro que não é destinado a novatos. Mas é bem bonito e a apresentação merece, de fato, o esforço de compreensão. Em princípio, tudo é explicado ainda que, certamente, as coisas às vezes sejam apresentadas rapidamente. Aqui ainda, as referências dadas poderão ser úteis no caso de dificuldades... Coragem e bom espectáculo!

Por último, o capítulo 9 é especial. Propõe uma prova de um teorema geométrico. Esta demonstração não utiliza nada de inacessível para o nível médio e este capítulo poderia ter sido colocado após o capítulo 1. A matemática não existiria se os teoremas não fossem demonstrados. Quisemos mostrar isso claramente no fim de um filme cujo objetivo é mostrar objetos matemáticos. (Ver aqui)

Eis aqui algumas possibilidades de percurso

Collégien: 1 ou 1-2 ou 1-2-9

Ensino fundamental : 1 ou 1-2 ou 1-2-9

Ensino médio :  1-2-(3-4)-9

Final do ensino médio: 5-6

Estudantes do ciclo básico da universidade : 2-3-4-5-6 ou 5-6-(7-8-9)

Estudantes dos últimos anos da universidade : 7-8-(9)

Público, em geral : 1-2-3-4-(9)