Jetez un oeil au contenu du film ou passez directement au guide d'utilisation du film .

Chapitre 1

La dimension deux

Hipparque explique comment localiser un lieu sur la Terre grâce à deux nombres...

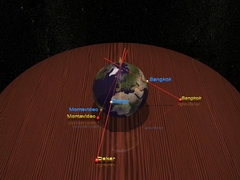... et nous enseigne la projection stéréographique : une méthode pour dessiner une carte du monde.

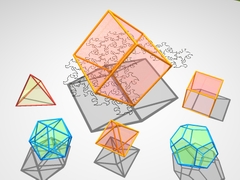
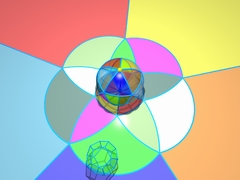
Chapitre 2

La dimension trois

M.C. Escher raconte les aventures de créatures de dimension 2 qui cherchent à imaginer des objets de dimension 3.

Chapitres 3 et 4

La quatrième dimension

Le mathématicien Ludwig Schläfli nous parle d'objets dans la quatrième dimension...

... et nous montre un défilé de polyèdres réguliers en dimension 4, objets étranges à 24, 120 et même 600 faces !

Chapitres 5 et 6

Les nombres complexes

Le mathématicien Adrien Douady explique les nombres complexes. La racine carrée des nombres négatifs expliquée simplement.

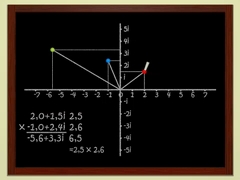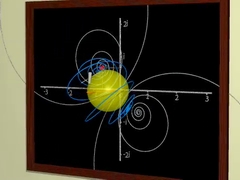
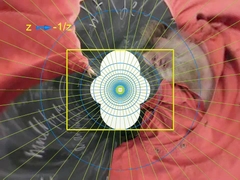
Transformer le plan, déformer des images, créer des images fractales...

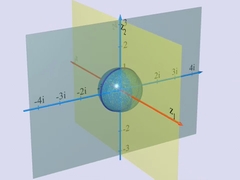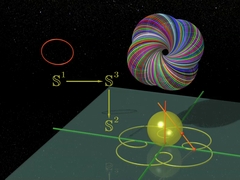
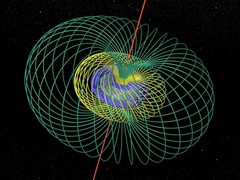
Chapitres 7 et 8

Fibration

Le mathématicien Heinz Hopf décrit sa "fibration". Grâce aux nombres complexes il construit de jolis arrangements de cercles dans l'espace.

Des cercles, des tores, le tout en rotation dans l'espace... de dimension 4 !

Chapitre 9

Une preuve mathématique

Le mathématicien Bernhard Riemann explique l'importance des démonstrations en mathématiques. Il démontre un théorème sur la projection stéréographique.

Comment utiliser ce film ?

Le film est conçu pour que tous les publics (qui le désirent !) puissent l'apprécier, à condition de bien choisir les chapitres. Il est constitué de neuf chapitres qui durent chacun treize minutes. En fait, les chapitres 3-4, 5-6 et 7-8 sont des chapitres doubles, mais à part cela, ils sont à peu près indépendants.

On peut bien sûr s'asseoir devant une télévision ou un ordinateur et regarder l'ensemble des 117 minutes d'une seule traite ! Mais il y aura peut-être des passages qui vous paraîtront trop rapides, ou au contraire trop élémentaires. Cela dépend de vos thèmes d'intérêt, de vos connaissances préalables, ou tout simplement de votre humeur du moment... On peut aussi se contenter de certains chapitres bien choisis. Voici quelques indications pour vous aider à tirer le meilleur parti possible du film. Pour en savoir un peu plus, on peut consulter les pages d'explications, où on trouve aussi de courts extraits du film..

Grosso modo, le niveau mathématique des chapitres va en augmentant peu à peu :

Le chapitre 1, la dimension 2, est très élémentaire. Il devrait pouvoir être apprécié par des élèves du collège mais nous pensons que même si vous savez déjà ce que sont les méridiens et les parallèles, vous aurez peut-être plaisir à voir le spectacle de la Terre qui roule comme une balle ! (Voir ici).

Le chapitre 2, la dimension 3, reste élémentaire mais demande un peu d'imagination. On peut très bien le regarder comme un spectacle, qui incite un peu à la philosophie... Il contient même des exercices, pour bien vérifier que vous avez compris. Pour des explications, des compléments, des références additionnelles, on peut consulter cette page sur ce site.

Les chapitres 3 et 4 nous présentent la quatrième dimension. C'est bien sûr plus difficile et vous serez peut-être pris de vertiges ? Si vous voulez tout comprendre, n'hésitez pas à utiliser la touche pause de votre télécommande, à revoir plusieurs fois ces chapitres, à consulter cette page dans lequel vous trouverez des références pour des compléments. Mais aussi, si vous n'avez pas envie de tout comprendre, vous pouvez tout simplement admirer les images !

Les chapitres 5 et 6, nombres complexes, proposent une introduction aux nombres complexes, qu'on apprend dans les classes terminales en France. Il ne s'agit pas de se substituer à un cours classique, mais nous pensons que ces chapitres pourraient en être d'agréables compléments. Si vous avez appris ce que sont les nombres complexes il y a longtemps, et que vous avez oublié..., ceci pourrait vous rafraîchir la mémoire. Si vous ne savez rien des nombres complexes, il vous faudra utiliser la touche pause plusieurs fois et chercher à comprendre en utilisant les références que nous proposons. Ces chapitres sont les plus "scolaires" du film. Pour vous remercier de l'effort fourni, la fin du chapitre 6 propose une scène de plongée époustouflante.

Les chapitres 7 et 8 contiennent une introduction à la fibration de Hopf, qui n'est pas discutée au lycée, ni même dans les premiers cycles universitaires. Il est donc clair qu'il n'est pas destiné à de vrais débutants. Mais c'est bien joli et le jeu mérite bien l'effort de compréhension. En principe, tout est expliqué même si, bien sûr, les choses vont parfois un peu vite. Ici encore, les références données pourront être utiles en cas de difficultés... Bon courage et bon spectacle !

Enfin, le chapitre 9 a un statut particulier. Il propose une preuve d'un théorème géométrique. Cette démonstration n'utilise rien d'inaccessible au niveau du collège et ce chapitre aurait pu être placé après le chapitre 1. Les mathématiques n'existeraient pas si les théorèmes n'étaient pas démontrés. Nous avons voulu exprimer cela clairement à la fin d'un film dont l'essentiel est de montrer des objets mathématiques. (Voir ici).

Voici quelques parcours possibles :

Collégien : 1 ou 1-2 ou 1-2-9
Lycéen : 1-2-(3-4)-9
Lycéen scientifique 5-6
Etudiant de premier cycle scientifique: 2-3-4-5-6 ou 5-6-(7-8-9)
Second cycle scientifique : 7-8-(9)
Public général : 1-2-3-4-(9)