Взгляните на краткое содержание фильма, или перейдите к гиду.

Глава 1

Размерность два

Гиппарх объясняет нам, как двумя числами задать положение любой точки Земли…

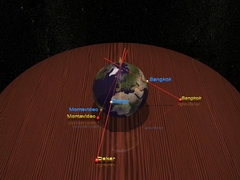… и обучает одному из способов рисовать карту мира — стереографической проекции.

Глава 2

Размерность три

М. К. Эшер описывает приключения двумерных существ, которые пытаются представить себе трёхмерные объекты.

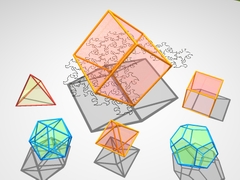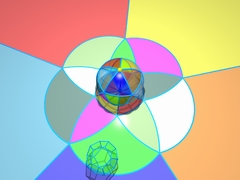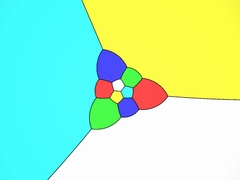Главы 3 и 4

Четвёртое измерение

Математик Людвиг Шлефли рассказывает об объектах, которые живут в четырёхмерном пространстве…

… мы оказываемся на параде правильных четырёхмерных многогранников, странных объектов с 24, 120 и даже 600 гранями!

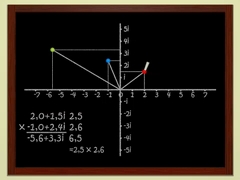
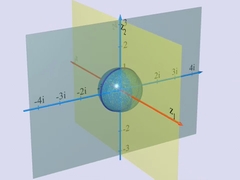
Главы 5 и 6

Комплексные числа

Математик Адриан Дуади объясняет, что такое комплексные числа. Он даёт простое объяснение того, что такое корень из отрицательного числа.

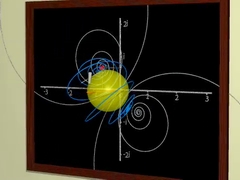
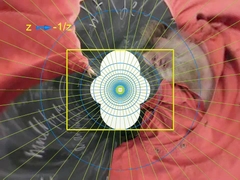
Преобразуем плоскость, деформируем изображения, создаём фрактальные рисунки…

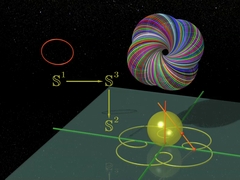
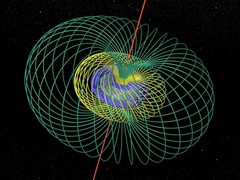
Главы 7 и 8

Расслоение

Математик Хейнц Хопф описывает своё расслоение. Используя комплексные числа, он красиво располагает окружности в пространстве.

Окружности, торы, и всё это вращается… в четырёхмерном пространстве.

Глава 9

Доказательство

Математик Бернхард Риман объясняет важность доказательств в математике. Он доказывает одну из теорем о стереографической проекции.

Как пользоваться этим фильмом?

Каждый (если захочет) может получить удовольствие от просмотра, надо только правильно выбрать, какие главы смотреть. Фильм состоит из 9 глав, по 13 минут каждая. Глава 4 является продолжением главы 3, глава 6 — главы 5, а глава 8 — главы 7. В остальном все главы более или менее не зависят друг от друга.

Конечно, можно сесть у телевизора или компьютера и просмотреть подряд все 117 минут фильма. Возможно, какие-то места покажутся вам слишком сложными, а другие, наоборот, слишком простыми. Это зависит от ваших интересов, ваших знаний, и даже просто от того, какое у вас в данный момент настроение! Можно, напротив, ограничиться несколькими правильно подобранными главами. Мы подготовили несколько советов, чтобы помочь вам извлечь из фильма всё самое лучшее. Вы можете узнать больше на страницах с описаниями глав, там же вы найдёте небольшие видеоролики с фрагментами из фильма.

В общих чертах, сложность глав постепенно возрастает.

Глава 1, размерность 2, очень простая. Её смогут понять ученики средней школы, и мы считаем, что даже если вы уже знаете, что такое меридианы и параллели, вы можете просто получить удовольствие от вида Земли, катящейся, словно мячик! (См. здесь)

Глава 2, размерность 3, всё ещё лёгкая, но всё-таки требует некоторого воображения. Её можно смотреть просто как спектакль, навевающий философское настроение. В ней даже есть упражнения, которые помогут вам проверить, действительно ли вы поняли эту главу. Дополнительные объяснения, информацию и справки вы можете найти на этой странице нашего сайта.

Главы 3 и 4 выведут нас в четвёртое измерение. Конечно, эти главы уже гораздо сложнее, и от них у вас может закружиться голова! Если вы хотите их понять, не стесняйтесь нажимать на кнопку пауза, пересматривать их по нескольку раз и читать эту страницу (на ней вы найдёте отсылки к дополнительной информации). Но даже если вы не хотите и пытаться всё это понять, вы можете просто откинуться на спинку стула и наслаждаться красивыми картинками.

Главы 5 и 6, комплексные числа, содержат введение в теорию комплексных чисел. Во Франции её изучают в старшем классе средней школы. Эти главы не заменяют классический школьный курсы, но, как нам кажется, могут быть хорошим дополнением к нему. Если вы изучали комплексные числа давно и многое уже забыли, эти главы помогут освежить вашу память. Если же вы, наоборот, ничего о них не знаете, почаще нажимайте кнопку пауза, и постарайтесь, используя нашу справочную информацию, понять, о чём идёт речь. Это наиболее школьные главы фильма. В награду за ваши старания 6-я глава заканчивается удивительным погружением в множество Мандельброта.

Главы 7 и 8 дадут вам первое представление о расслоении Хопфа, которое не проходят ни в школе, ни даже на первых курсах института. Эти главы рассчитаны уж точно не на новичка! Хотя сюжет очень милый, и стоит попытаться его понять. В видеоролике всё объяснено, но, конечно, местами повествование может идти слишком быстро для вас. Как обычно, в понимании может помочь наша справка. Удачи и приятного просмотра!

Наконец, глава 9 занимает особое место. В ней рассказано доказательство геометрической теоремы. Для понимания доказательства не нужно знать что-либо выходящее за границы школьного курса математики, и мы вполне могли бы поместить эту главу сразу после первой. Без доказательств математики бы не существовало. Мы хотели подчеркнуть это в конце фильма, который в основном посвящён математическим объектам. (Смотрите здесь).

Вот возможные варианты выбора глав:

Младшая средняя школа (12-15 лет): 1 или 1-2 или 1-2-9
Старшая средняя школа (16-18 лет): 1-2-(3-4)-9
Старшая средняя школа с математическим профилем: 5-6
Начальные курсы технического института: 2-3-4-5 или 5-6-(7-8-9)
Старшие курсы технического института: 7-8-(9)
Широкая публика: 1-2-3-4-(9)